ベイズ理論とはデータによって「もとの確率」がどう変化するかを示す理論です。たとえば、肝線維化病期はF0からF4 までの5段階で表現されます。検査前には、どの病期に当てはまるかは全く分かりません。つまりF0である確率もF4である確率も同じであると言えます(一様分布)。この症例に対してエラストグラフィを施行すると、5kPaという結果を得たとしましょう。5kPa というと病期F4(肝硬変)の平均的な硬さよりも高い値です。この結果は「この症例の病期がF4である可能性が高い」ことを示します。しかし何パーセントの確率でF4と言えるのでしょうか? この答えを与えるのがベイズ理論です1。ベイズの定理から推定して、この症例が病期F4である確率は85%、病期F3の確率は15%と定量的に示すことができます。また、この症例に対して追加で検査を行ったらその確信度はさらに高まり100%近くになるかもしれません。この場合にもベイズ理論が適応できます。ベイズ理論ではデータを追加することで、確率(確信度)を「更新」することができるからです。
ベイズ理論のアプローチに必要なのは、過去データの調査だけです。この例の場合では各線維化病期に属する症例のエラストグラフィ検査の集計値(平均値と標準偏差)です。ひとたび多数例での調査が行われれば、その調査結果を今後の症例に生かすことができます。過去に得た研究結果を、いま目の前にいる症例に適応できるのです。ベイズ理論は医療研究と臨床をつなぐアプローチです。
我々はベイズ理論を肝線維化推定に応用するための簡易プログラムを公開しています。Baysianのホームページ »
- Motosugi U, et al. Bayesian prediction for liver fibrosis staging: combined use of elastography and serum fibrosis markers. Hepatology 2013 Jul;58(1):450-1.
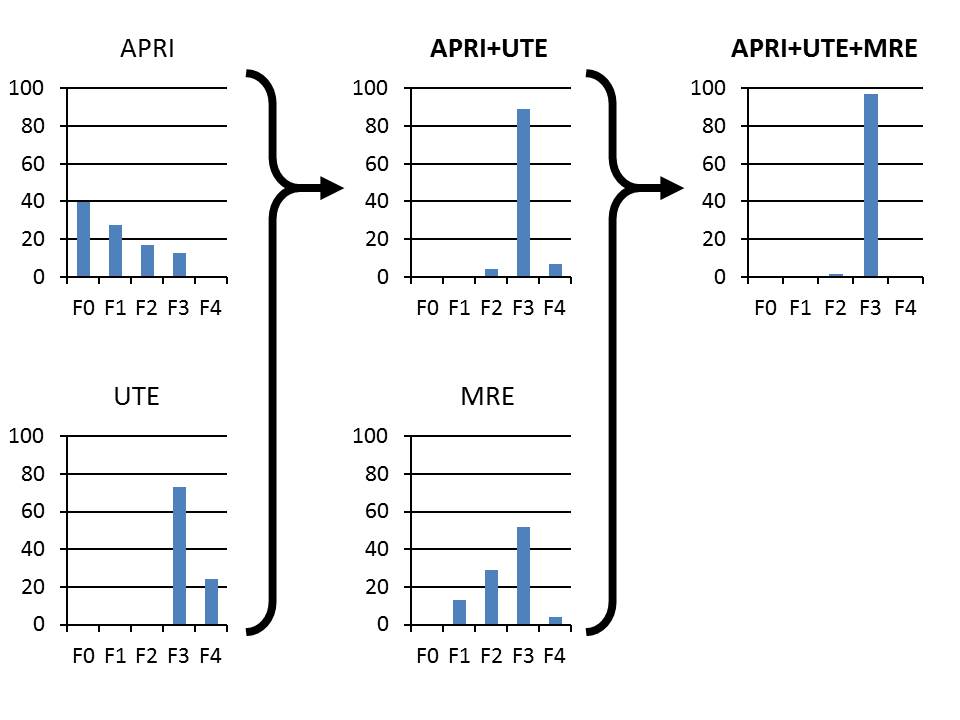
APRIとは血小板値とAST値を用いた肝線維化マーカです。簡便であるが精度に欠けます。UTEは超音波エラストグラフィ、MREはMRエラストグラフィです。
APRI単独ではどの線維化病期か判然としません(左上)。UTE単独ではF3である確率が7割程度です(左下)。UTEとARFIを合わせるとF3である確率が8割を超えます。さらにMREを加えることで、95%の確信度で「この症例はF3である」と推定できます。これはARFI,UTE,MREの3つを統合した結果です。簡便な検査から始め、臨床的に必要な確信度が得られるまで検査を追加します。これは日常臨床のアプローチそのものです。

